-9.3 C
New York
Monday, December 23, 2024
HomeArtificial Intelligence
Artificial Intelligence

Experimenting with autoregressive flows in TensorFlow Likelihood

By admin
0
12
Experimenting with autoregressive flows in TensorFlow Likelihood



Experimenting with autoregressive flows in TensorFlow Likelihood

Within the first a part of this mini-series on autoregressive movement fashions, we checked out bijectors in TensorFlow Likelihood (TFP), and noticed use them for sampling and density estimation. We singled out the affine bijector to exhibit the mechanics of movement building: We begin from a distribution that’s straightforward to pattern from, and that permits for simple calculation of its density. Then, we connect some variety of invertible transformations, optimizing for data-likelihood underneath the ultimate reworked distribution. The effectivity of that (log)chance calculation is the place normalizing flows excel: Loglikelihood underneath the (unknown) goal distribution is obtained as a sum of the density underneath the bottom distribution of the inverse-transformed knowledge plus absolutely the log determinant of the inverse Jacobian.

Now, an affine movement will seldom be highly effective sufficient to mannequin nonlinear, complicated transformations. In constrast, autoregressive fashions have proven substantive success in density estimation in addition to pattern era. Mixed with extra concerned architectures, function engineering, and in depth compute, the idea of autoregressivity has powered – and is powering – state-of-the-art architectures in areas similar to picture, speech and video modeling.

This put up can be involved with the constructing blocks of autoregressive flows in TFP. Whereas we received’t precisely be constructing state-of-the-art fashions, we’ll attempt to perceive and play with some main elements, hopefully enabling the reader to do her personal experiments on her personal knowledge.

This put up has three elements: First, we’ll take a look at autoregressivity and its implementation in TFP. Then, we attempt to (roughly) reproduce one of many experiments within the “MAF paper” (Masked Autoregressive Flows for Distribution Estimation (Papamakarios, Pavlakou, and Murray 2017)) – primarily a proof of idea. Lastly, for the third time on this weblog, we come again to the duty of analysing audio knowledge, with combined outcomes.

Autoregressivity and masking

In distribution estimation, autoregressivity enters the scene by way of the chain rule of likelihood that decomposes a joint density right into a product of conditional densities:

[
p(mathbf{x}) = prod_{i}p(mathbf{x}_i|mathbf{x}_{1:i−1})
]

In observe, because of this autoregressive fashions should impose an order on the variables – an order which could or may not “make sense.” Approaches right here embrace selecting orderings at random and/or utilizing totally different orderings for every layer.
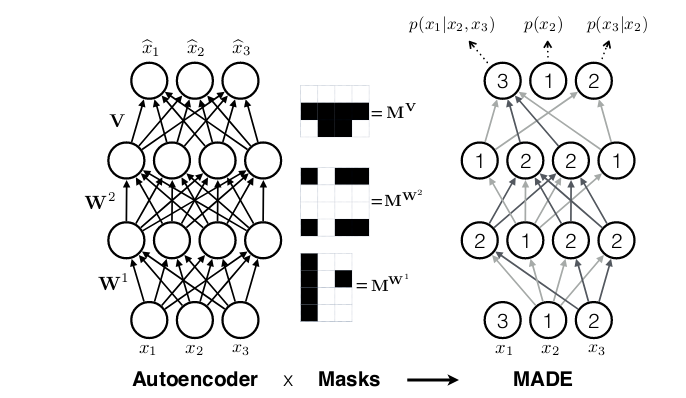
Whereas in recurrent neural networks, autoregressivity is conserved as a result of recurrence relation inherent in state updating, it isn’t clear a priori how autoregressivity is to be achieved in a densely linked structure. A computationally environment friendly answer was proposed in MADE: Masked Autoencoder for Distribution Estimation(Germain et al. 2015): Ranging from a densely linked layer, masks out all connections that shouldn’t be allowed, i.e., all connections from enter function (i) to mentioned layer’s activations (1 … i-1). Or expressed in a different way, activation (i) could also be linked to enter options (1 … i-1) solely. Then when including extra layers, care have to be taken to make sure that all required connections are masked in order that on the finish, output (i) will solely ever have seen inputs (1 … i-1).

Thus masked autoregressive flows are a fusion of two main approaches – autoregressive fashions (which needn’t be flows) and flows (which needn’t be autoregressive). In TFP these are supplied by MaskedAutoregressiveFlow, for use as a bijector in a TransformedDistribution.

Whereas the documentation exhibits use this bijector, the step from theoretical understanding to coding a “black field” could seem broad. In the event you’re something just like the writer, right here you may really feel the urge to “look underneath the hood” and confirm that issues actually are the way in which you’re assuming. So let’s give in to curiosity and permit ourselves a bit of escapade into the supply code.

Peeking forward, that is how we’ll assemble a masked autoregressive movement in TFP (once more utilizing the nonetheless new-ish R bindings supplied by tfprobability):

library(tfprobability)

maf <- tfb_masked_autoregressive_flow(
    shift_and_log_scale_fn = tfb_masked_autoregressive_default_template(
      hidden_layers = listing(num_hidden, num_hidden),
      activation = tf$nn$tanh)
)

Pulling aside the related entities right here, tfb_masked_autoregressive_flow is a bijector, with the standard strategies tfb_forward(), tfb_inverse(), tfb_forward_log_det_jacobian() and tfb_inverse_log_det_jacobian().
The default shift_and_log_scale_fn, tfb_masked_autoregressive_default_template, constructs a bit of neural community of its personal, with a configurable variety of hidden models per layer, a configurable activation operate and optionally, different configurable parameters to be handed to the underlying dense layers. It’s these dense layers that should respect the autoregressive property. Can we check out how that is carried out? Sure we will, supplied we’re not afraid of a bit of Python.

masked_autoregressive_default_template (now leaving out the tfb_ as we’ve entered Python-land) makes use of masked_dense to do what you’d suppose a thus-named operate could be doing: assemble a dense layer that has a part of the burden matrix masked out. How? We’ll see after just a few Python setup statements.

present type on grasp), and when attainable, simplified for higher readability, accommodating simply the specifics of the chosen instance – a toy matrix of form 2×3:

Papamakarios, Pavlakou, and Murray 2017) utilized masked autoregressive flows (in addition to single-layer-MADE(Germain et al. 2015) and Actual NVP (Dinh, Sohl-Dickstein, and Bengio 2016)) to quite a lot of datasets, together with MNIST, CIFAR-10 and a number of other datasets from the UCI Machine Studying Repository.

We choose one of many UCI datasets: Fuel sensors for dwelling exercise monitoring. On this dataset, the MAF authors obtained the very best outcomes utilizing a MAF with 10 flows, so that is what we are going to attempt.

Amassing info from the paper, we all know that

  • knowledge was included from the file ethylene_CO.txt solely;
  • discrete columns have been eradicated, in addition to all columns with correlations > .98; and
  • the remaining 8 columns have been standardised (z-transformed).

Relating to the neural community structure, we collect that

  • every of the ten MAF layers was adopted by a batchnorm;
  • as to function order, the primary MAF layer used the variable order that got here with the dataset; then each consecutive layer reversed it;
  • particularly for this dataset and versus all different UCI datasets, tanh was used for activation as a substitute of relu;
  • the Adam optimizer was used, with a studying charge of 1e-4;
  • there have been two hidden layers for every MAF, with 100 models every;
  • coaching went on till no enchancment occurred for 30 consecutive epochs on the validation set; and
  • the bottom distribution was a multivariate Gaussian.

That is all helpful info for our try to estimate this dataset, however the important bit is that this. In case you knew the dataset already, you might need been questioning how the authors would take care of the dimensionality of the information: It’s a time sequence, and the MADE structure explored above introduces autoregressivity between options, not time steps. So how is the extra temporal autoregressivity to be dealt with? The reply is: The time dimension is basically eliminated. Within the authors’ phrases,

[…] it’s a time sequence however was handled as if every instance have been an i.i.d. pattern from the marginal distribution.

This undoubtedly is beneficial info for our current modeling try, however it additionally tells us one thing else: We’d should look past MADE layers for precise time sequence modeling.

Now although let’s take a look at this instance of utilizing MAF for multivariate modeling, with no time or spatial dimension to be taken into consideration.

Following the hints the authors gave us, that is what we do.

Observations: 4,208,261
Variables: 19
$ X1  <dbl> 0.00, 0.01, 0.01, 0.03, 0.04, 0.05, 0.06, 0.07, 0.07, 0.09,...
$ X2  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,...
$ X3  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,...
$ X4  <dbl> -50.85, -49.40, -40.04, -47.14, -33.58, -48.59, -48.27, -47.14,... 
$ X5  <dbl> -1.95, -5.53, -16.09, -10.57, -20.79, -11.54, -9.11, -4.56,...
$ X6  <dbl> -41.82, -42.78, -27.59, -32.28, -33.25, -36.16, -31.31, -16.57,... 
$ X7  <dbl> 1.30, 0.49, 0.00, 4.40, 6.03, 6.03, 5.37, 4.40, 23.98, 2.77,...
$ X8  <dbl> -4.07, 3.58, -7.16, -11.22, 3.42, 0.33, -7.97, -2.28, -2.12,...
$ X9  <dbl> -28.73, -34.55, -42.14, -37.94, -34.22, -29.05, -30.34, -24.35,...
$ X10 <dbl> -13.49, -9.59, -12.52, -7.16, -14.46, -16.74, -8.62, -13.17,...
$ X11 <dbl> -3.25, 5.37, -5.86, -1.14, 8.31, -1.14, 7.00, -6.34, -0.81,...
$ X12 <dbl> 55139.95, 54395.77, 53960.02, 53047.71, 52700.28, 51910.52,...
$ X13 <dbl> 50669.50, 50046.91, 49299.30, 48907.00, 48330.96, 47609.00,...
$ X14 <dbl> 9626.26, 9433.20, 9324.40, 9170.64, 9073.64, 8982.88, 8860.51,...
$ X15 <dbl> 9762.62, 9591.21, 9449.81, 9305.58, 9163.47, 9021.08, 8966.48,...
$ X16 <dbl> 24544.02, 24137.13, 23628.90, 23101.66, 22689.54, 22159.12,...
$ X17 <dbl> 21420.68, 20930.33, 20504.94, 20101.42, 19694.07, 19332.57,...
$ X18 <dbl> 7650.61, 7498.79, 7369.67, 7285.13, 7156.74, 7067.61, 6976.13,...
$ X19 <dbl> 6928.42, 6800.66, 6697.47, 6578.52, 6468.32, 6385.31, 6300.97,...
# we do not know if we'll find yourself with the identical columns because the authors did,
# however we attempt (no less than we do find yourself with 8 columns)
df <- df[,-(1:3)]
hc <- findCorrelation(cor(df), cutoff = 0.985)
df2 <- df[,-c(hc)]

# scale
df2 <- scale(df2)
df2
# A tibble: 4,208,261 x 8
      X4     X5     X8    X9    X13    X16    X17   X18
   <dbl>  <dbl>  <dbl> <dbl>  <dbl>  <dbl>  <dbl> <dbl>
 1 -50.8  -1.95  -4.07 -28.7 50670. 24544. 21421. 7651.
 2 -49.4  -5.53   3.58 -34.6 50047. 24137. 20930. 7499.
 3 -40.0 -16.1   -7.16 -42.1 49299. 23629. 20505. 7370.
 4 -47.1 -10.6  -11.2  -37.9 48907  23102. 20101. 7285.
 5 -33.6 -20.8    3.42 -34.2 48331. 22690. 19694. 7157.
 6 -48.6 -11.5    0.33 -29.0 47609  22159. 19333. 7068.
 7 -48.3  -9.11  -7.97 -30.3 47047. 21932. 19028. 6976.
 8 -47.1  -4.56  -2.28 -24.4 46758. 21504. 18780. 6900.
 9 -42.3  -2.77  -2.12 -27.6 46197. 21125. 18439. 6827.
10 -44.6   3.58  -0.65 -35.5 45652. 20836. 18209. 6790.
# … with 4,208,251 extra rows

Now arrange the information era course of:

# train-test break up
n_rows <- nrow(df2) # 4208261
train_ids <- pattern(1:n_rows, 0.5 * n_rows)
x_train <- df2[train_ids, ]
x_test <- df2[-train_ids, ]

# create datasets
batch_size <- 100
train_dataset <- tf$solid(x_train, tf$float32) %>%
  tensor_slices_dataset %>%
  dataset_batch(batch_size)

test_dataset <- tf$solid(x_test, tf$float32) %>%
  tensor_slices_dataset %>%
  dataset_batch(nrow(x_test))

To assemble the movement, the very first thing wanted is the bottom distribution.

base_dist <- tfd_multivariate_normal_diag(loc = rep(0, ncol(df2)))

Now for the movement, by default constructed with batchnorm and permutation of function order.

num_hidden <- 100
dim <- ncol(df2)

use_batchnorm <- TRUE
use_permute <- TRUE
num_mafs <-10
num_layers <- 3 * num_mafs

bijectors <- vector(mode = "listing", size = num_layers)

for (i in seq(1, num_layers, by = 3)) {
  maf <- tfb_masked_autoregressive_flow(
    shift_and_log_scale_fn = tfb_masked_autoregressive_default_template(
      hidden_layers = listing(num_hidden, num_hidden),
      activation = tf$nn$tanh))
  bijectors[[i]] <- maf
  if (use_batchnorm)
    bijectors[[i + 1]] <- tfb_batch_normalization()
  if (use_permute)
    bijectors[[i + 2]] <- tfb_permute((ncol(df2) - 1):0)
}

if (use_permute) bijectors <- bijectors[-num_layers]

movement <- bijectors %>%
  discard(is.null) %>%
  # tfb_chain expects arguments in reverse order of software
  rev() %>%
  tfb_chain()

target_dist <- tfd_transformed_distribution(
  distribution = base_dist,
  bijector = movement
)

And configuring the optimizer:

optimizer <- tf$prepare$AdamOptimizer(1e-4)

Below that isotropic Gaussian we selected as a base distribution, how seemingly are the information?

base_loglik <- base_dist %>% 
  tfd_log_prob(x_train) %>% 
  tf$reduce_mean()
base_loglik %>% as.numeric()        # -11.33871

base_loglik_test <- base_dist %>% 
  tfd_log_prob(x_test) %>% 
  tf$reduce_mean()
base_loglik_test %>% as.numeric()   # -11.36431

And, simply as a fast sanity examine: What’s the loglikelihood of the information underneath the reworked distribution earlier than any coaching?

target_loglik_pre <-
  target_dist %>% tfd_log_prob(x_train) %>% tf$reduce_mean()
target_loglik_pre %>% as.numeric()        # -11.22097

target_loglik_pre_test <-
  target_dist %>% tfd_log_prob(x_test) %>% tf$reduce_mean()
target_loglik_pre_test %>% as.numeric()   # -11.36431

The values match – good. Right here now could be the coaching loop. Being impatient, we already hold checking the loglikelihood on the (full) check set to see if we’re making any progress.

n_epochs <- 10

for (i in 1:n_epochs) {
  
  agg_loglik <- 0
  num_batches <- 0
  iter <- make_iterator_one_shot(train_dataset)
  
  until_out_of_range({
    batch <- iterator_get_next(iter)
    loss <-
      operate()
        - tf$reduce_mean(target_dist %>% tfd_log_prob(batch))
    optimizer$decrease(loss)
    
    loglik <- tf$reduce_mean(target_dist %>% tfd_log_prob(batch))
    agg_loglik <- agg_loglik + loglik
    num_batches <- num_batches + 1
    
    test_iter <- make_iterator_one_shot(test_dataset)
    test_batch <- iterator_get_next(test_iter)
    loglik_test_current <- target_dist %>% tfd_log_prob(test_batch) %>% tf$reduce_mean()
    
    if (num_batches %% 100 == 1)
      cat(
        "Epoch ",
        i,
        ": ",
        "Batch ",
        num_batches,
        ": ",
        (agg_loglik %>% as.numeric()) / num_batches,
        " --- check: ",
        loglik_test_current %>% as.numeric(),
        "n"
      )
  })
}

With each coaching and check units amounting to over 2 million data every, we didn’t have the persistence to run this mannequin till no enchancment occurred for 30 consecutive epochs on the validation set (just like the authors did). Nonetheless, the image we get from one full epoch’s run is fairly clear: The setup appears to work fairly okay.

Epoch  1 :  Batch      1:  -8.212026  --- check:  -10.09264 
Epoch  1 :  Batch   1001:   2.222953  --- check:   1.894102 
Epoch  1 :  Batch   2001:   2.810996  --- check:   2.147804 
Epoch  1 :  Batch   3001:   3.136733  --- check:   3.673271 
Epoch  1 :  Batch   4001:   3.335549  --- check:   4.298822 
Epoch  1 :  Batch   5001:   3.474280  --- check:   4.502975 
Epoch  1 :  Batch   6001:   3.606634  --- check:   4.612468 
Epoch  1 :  Batch   7001:   3.695355  --- check:   4.146113 
Epoch  1 :  Batch   8001:   3.767195  --- check:   3.770533 
Epoch  1 :  Batch   9001:   3.837641  --- check:   4.819314 
Epoch  1 :  Batch  10001:   3.908756  --- check:   4.909763 
Epoch  1 :  Batch  11001:   3.972645  --- check:   3.234356 
Epoch  1 :  Batch  12001:   4.020613  --- check:   5.064850 
Epoch  1 :  Batch  13001:   4.067531  --- check:   4.916662 
Epoch  1 :  Batch  14001:   4.108388  --- check:   4.857317 
Epoch  1 :  Batch  15001:   4.147848  --- check:   5.146242 
Epoch  1 :  Batch  16001:   4.177426  --- check:   4.929565 
Epoch  1 :  Batch  17001:   4.209732  --- check:   4.840716 
Epoch  1 :  Batch  18001:   4.239204  --- check:   5.222693 
Epoch  1 :  Batch  19001:   4.264639  --- check:   5.279918 
Epoch  1 :  Batch  20001:   4.291542  --- check:   5.29119 
Epoch  1 :  Batch  21001:   4.314462  --- check:   4.872157 
Epoch  2 :  Batch      1:   5.212013  --- check:   4.969406

With these coaching outcomes, we regard the proof of idea as principally profitable. Nonetheless, from our experiments we additionally should say that the selection of hyperparameters appears to matter a lot. For instance, use of the relu activation operate as a substitute of tanh resulted within the community principally studying nothing. (As per the authors, relu labored effective on different datasets that had been z-transformed in simply the identical method.)

Batch normalization right here was compulsory – and this may go for flows generally. The permutation bijectors, then again, didn’t make a lot of a distinction on this dataset. Total the impression is that for flows, we’d both want a “bag of tips” (like is usually mentioned about GANs), or extra concerned architectures (see “Outlook” under).

Lastly, we wind up with an experiment, coming again to our favourite audio knowledge, already featured in two posts: Easy Audio Classification with Keras and Audio classification with Keras: Trying nearer on the non-deep studying elements.

Analysing audio knowledge with MAF

The dataset in query consists of recordings of 30 phrases, pronounced by quite a lot of totally different audio system. In these earlier posts, a convnet was educated to map spectrograms to these 30 lessons. Now as a substitute we wish to attempt one thing totally different: Practice an MAF on one of many lessons – the phrase “zero,” say – and see if we will use the educated community to mark “non-zero” phrases as much less seemingly: carry out anomaly detection, in a method. Spoiler alert: The outcomes weren’t too encouraging, and in case you are serious about a job like this, you may wish to think about a distinct structure (once more, see “Outlook” under).

Nonetheless, we shortly relate what was carried out, as this job is a pleasant instance of dealing with knowledge the place options range over multiple axis.

Preprocessing begins as within the aforementioned earlier posts. Right here although, we explicitly use keen execution, and will typically hard-code identified values to maintain the code snippets brief.

Audio classification with Keras: Trying nearer on the non-deep studying elements, we’d like to coach the community on spectrograms as a substitute of the uncooked time area knowledge.
Utilizing the identical settings for frame_length and frame_step of the Brief Time period Fourier Rework as in that put up, we’d arrive at knowledge formed variety of frames x variety of FFT coefficients. To make this work with the masked_dense() employed in tfb_masked_autoregressive_flow(), the information would then should be flattened, yielding a powerful 25186 options within the joint distribution.

With the structure outlined as above within the GAS instance, this result in the community not making a lot progress. Neither did leaving the information in time area type, with 16000 options within the joint distribution. Thus, we determined to work with the FFT coefficients computed over the whole window as a substitute, leading to 257 joint options.

batch_size <- 100

sampling_rate <- 16000L
data_generator <- operate(df,
                           batch_size) {
  
  ds <- tensor_slices_dataset(df) 
  
  ds <- ds %>%
    dataset_map(operate(obs) {
      wav <-
        decode_wav()(tf$read_file(tf$reshape(obs$fname, listing())))
      samples <- wav$audio[ ,1]
      
      # some wave recordsdata have fewer than 16000 samples
      padding <- listing(listing(0L, sampling_rate - tf$form(samples)[1]))
      padded <- tf$pad(samples, padding)
      
      stft_out <- stft()(padded, 16000L, 1L, 512L)
      magnitude_spectrograms <- tf$abs(stft_out) %>% tf$squeeze()
    })
  
  ds %>% dataset_batch(batch_size)
  
}

ds_train <- data_generator(df_train, batch_size)
batch <- ds_train %>% 
  make_iterator_one_shot() %>%
  iterator_get_next()

dim(batch) # 100 x 257

Coaching then proceeded as on the GAS dataset.

# outline MAF
base_dist <-
  tfd_multivariate_normal_diag(loc = rep(0, dim(batch)[2]))

num_hidden <- 512 
use_batchnorm <- TRUE
use_permute <- TRUE
num_mafs <- 10 
num_layers <- 3 * num_mafs

# retailer bijectors in a listing
bijectors <- vector(mode = "listing", size = num_layers)

# fill listing, optionally including batchnorm and permute bijectors
for (i in seq(1, num_layers, by = 3)) {
  maf <- tfb_masked_autoregressive_flow(
    shift_and_log_scale_fn = tfb_masked_autoregressive_default_template(
      hidden_layers = listing(num_hidden, num_hidden),
      activation = tf$nn$tanh,
      ))
  bijectors[[i]] <- maf
  if (use_batchnorm)
    bijectors[[i + 1]] <- tfb_batch_normalization()
  if (use_permute)
    bijectors[[i + 2]] <- tfb_permute((dim(batch)[2] - 1):0)
}

if (use_permute) bijectors <- bijectors[-num_layers]
movement <- bijectors %>%
  # presumably clear out empty components (if no batchnorm or no permute)
  discard(is.null) %>%
  rev() %>%
  tfb_chain()

target_dist <- tfd_transformed_distribution(distribution = base_dist,
                                            bijector = movement)

optimizer <- tf$prepare$AdamOptimizer(1e-3)

# prepare MAF
n_epochs <- 100
for (i in 1:n_epochs) {
  agg_loglik <- 0
  num_batches <- 0
  iter <- make_iterator_one_shot(ds_train)
  until_out_of_range({
    batch <- iterator_get_next(iter)
    loss <-
      operate()
        - tf$reduce_mean(target_dist %>% tfd_log_prob(batch))
    optimizer$decrease(loss)
    
    loglik <- tf$reduce_mean(target_dist %>% tfd_log_prob(batch))
    agg_loglik <- agg_loglik + loglik
    num_batches <- num_batches + 1
    
    loglik_test_current <- 
      target_dist %>% tfd_log_prob(ds_test) %>% tf$reduce_mean()

    if (num_batches %% 20 == 1)
      cat(
        "Epoch ",
        i,
        ": ",
        "Batch ",
        num_batches,
        ": ",
        ((agg_loglik %>% as.numeric()) / num_batches) %>% spherical(1),
        " --- check: ",
        loglik_test_current %>% as.numeric() %>% spherical(1),
        "n"
      )
  })
}

Throughout coaching, we additionally monitored loglikelihoods on three totally different lessons, cat, hen and wow. Listed below are the loglikelihoods from the primary 10 epochs. “Batch” refers back to the present coaching batch (first batch within the epoch), all different values refer to finish datasets (the whole check set and the three units chosen for comparability).

epoch   |   batch  |   check   |   "cat"  |   "hen"  |   "wow"  |
--------|----------|----------|----------|-----------|----------|
1       |   1443.5 |   1455.2 |   1398.8 |    1434.2 |   1546.0 |
2       |   1935.0 |   2027.0 |   1941.2 |    1952.3 |   2008.1 | 
3       |   2004.9 |   2073.1 |   2003.5 |    2000.2 |   2072.1 |
4       |   2063.5 |   2131.7 |   2056.0 |    2061.0 |   2116.4 |        
5       |   2120.5 |   2172.6 |   2096.2 |    2085.6 |   2150.1 |
6       |   2151.3 |   2206.4 |   2127.5 |    2110.2 |   2180.6 | 
7       |   2174.4 |   2224.8 |   2142.9 |    2163.2 |   2195.8 |
8       |   2203.2 |   2250.8 |   2172.0 |    2061.0 |   2221.8 |        
9       |   2224.6 |   2270.2 |   2186.6 |    2193.7 |   2241.8 |
10      |   2236.4 |   2274.3 |   2191.4 |    2199.7 |   2243.8 |

Whereas this doesn’t look too dangerous, a whole comparability in opposition to all twenty-nine non-target lessons had “zero” outperformed by seven different lessons, with the remaining twenty-two decrease in loglikelihood. We don’t have a mannequin for anomaly detection, as but.

Outlook

As already alluded to a number of occasions, for knowledge with temporal and/or spatial orderings extra advanced architectures could show helpful. The very profitable PixelCNN household relies on masked convolutions, with more moderen developments bringing additional refinements (e.g. Gated PixelCNN (Oord et al. 2016), PixelCNN++ (Salimans et al. 2017). Consideration, too, could also be masked and thus rendered autoregressive, as employed within the hybrid PixelSNAIL (Chen et al. 2017) and the – not surprisingly given its title – transformer-based ImageTransformer (Parmar et al. 2018).

To conclude, – whereas this put up was within the intersection of flows and autoregressivity – and final not least the use therein of TFP bijectors – an upcoming one may dive deeper into autoregressive fashions particularly… and who is aware of, maybe come again to the audio knowledge for a fourth time.

Chen, Xi, Nikhil Mishra, Mostafa Rohaninejad, and Pieter Abbeel. 2017. “PixelSNAIL: An Improved Autoregressive Generative Mannequin.” CoRR abs/1712.09763. http://arxiv.org/abs/1712.09763.
Dinh, Laurent, Jascha Sohl-Dickstein, and Samy Bengio. 2016. “Density Estimation Utilizing Actual NVP.” CoRR abs/1605.08803. http://arxiv.org/abs/1605.08803.
Germain, Mathieu, Karol Gregor, Iain Murray, and Hugo Larochelle. 2015. “MADE: Masked Autoencoder for Distribution Estimation.” CoRR abs/1502.03509. http://arxiv.org/abs/1502.03509.
Oord, Aaron van den, Nal Kalchbrenner, Oriol Vinyals, Lasse Espeholt, Alex Graves, and Koray Kavukcuoglu. 2016. “Conditional Picture Technology with PixelCNN Decoders.” CoRR abs/1606.05328. http://arxiv.org/abs/1606.05328.
Papamakarios, George, Theo Pavlakou, and Iain Murray. 2017. “Masked Autoregressive Movement for Density Estimation.” arXiv e-Prints, Might, arXiv:1705.07057. https://arxiv.org/abs/1705.07057.
Parmar, Niki, Ashish Vaswani, Jakob Uszkoreit, Lukasz Kaiser, Noam Shazeer, and Alexander Ku. 2018. “Picture Transformer.” CoRR abs/1802.05751. http://arxiv.org/abs/1802.05751.
Salimans, Tim, Andrej Karpathy, Xi Chen, and Diederik P. Kingma. 2017. “PixelCNN++: Enhancing the PixelCNN with Discretized Logistic Combination Probability and Different Modifications.” CoRR abs/1701.05517. http://arxiv.org/abs/1701.05517.

Previous article
2024 yr in evaluate: From AI to Trump, what’s going to historical past keep in mind?
Next article
New Cisco CCT Area Technician Certification: Making ready for the Way forward for IT
adminhttp://itechepic.com

Related Articles

LEAVE A REPLY

Please enter your comment!
Please enter your name here

Latest Articles

Load more

iTechepic is your technology, AI, and big data related website. We provide you with the latest breaking news and videos straight from the tech industry.

© Copyright 2024 - itechepic.com. All rights reserved.